Recently, I have discovered a nice tiny library (1 file!) that supports Backtrack Programming in standard C. The library is called CBack and is developed by Keld Helsgaun, who is known in the Operations Research and Computer Science communities for his efficient implementation of the Lin-Kernighan heuristics for the Travelling Salesman Problem.

CBack offers basically two functions that are described in [1] as follows:

1. Choice(N): “is used when a choice is to be made among a number of alternatives, where N is a positive integer denoting the number of alternatives”.
2. Backtrack(): “causes the program to backtrack, that is to say, return to the most recent call of Choice, which has not yet returned all its values”.

With these two functions is pretty simple to develop exact enumeration algorithms. The CBack library comes with several examples, such as algorithms for the N-queens problem and the 15-puzzle. Below, I will show you how to use CBack to implement a simple algorithm that finds a Maximum Clique in an undirected graph.

As usual, the source code used to write this post is publicly available on my GitHub repository.

Basic use of CBack

The CBack documentation shows as first example the following code snippet:

1
2
3
4
5

int i, j;
i = Choice(3);
j = Choice(2);
printf("i = %d, j = %d\n",i,j);
Backtrack();

The output produced by the snippet is:

1
2
3
4
5
6

i = 1, j = 1
i = 1, j = 2
i = 2, j = 1
i = 2, j = 2
i = 3, j = 1
i = 3, j = 2

If you are familiar with backtrack programming (e.g., Prolog), you should not be surprised by the output, and you can jump to the next section. Otherwise, the Figure below sketches the program execution.

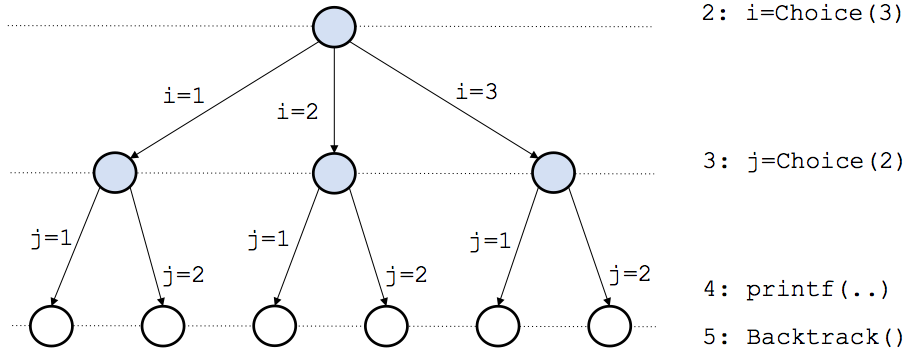
When the program executes the Choice(N=3) statement, that is the first call to the first choice (line 2), value 1 is assigned to variable i. Behind the scene, the Choice function stores the current execution state of the program in its own stack, and records the next possible choices (i.e. the other possible program branches), that are values 2 and 3. Next, the second Choice(N=2) assigns value 1 to j (line 3), and again the state of the program is stored for later use. Then, the printf outputs i = 1 , j = 1 (line 4 and first line of output). Now, it is time to backtrack (line 5).

What is happening here?

Look again at the figure above: When the Backtrack() function is invoked, the algorithm backtracks and continues the execution from the most recent Choice stored in its stack, i.e. it assigns to variable j value 2, and printf outputs i = 1, j = 2. Later, the Backtrack() is invoked again, and this time the algorithm backtracks until the previous possible choice that corresponds to the assignment of value 2 to variable i, and it executes i = 2. Once the second choice for variable i is performed, there are again two possible choices for variable j, since the program has backtracked to a point that precedes that statement. Thus, the program executes j = 1, and printf outputs i = 2, j = 1. At this point, the program backtracks again, and consider the next possible choice, j = 2. This is repeated until all possible choices for Choice(3) and Choice(2) are exhausted, yielding the 6 possible combinations of i and j that the problem gave as output.

Indeed, during the execution, the program has implicitly visited in a depth-first manner the search tree of the previous figure. CBack supports also different search strategy, such as best first, but I will not cover that topic here.

In order to store and restore the program execution state (well, more precisely the calling environment), Choice(N) and Backtrack use two threatening C standard functions, setjmp and longjmp. For the details of their use in CBack, see [1].

A Basic Maximum Clique Algorithm

The reason why I like this library, apart from remembering me the time I was programming with Mozart, is that it permits to implement quickly exact algorithms based on enumeration. While enumeration is usually disregarded as inefficient (“ehi, it is just brute force!”), it is still one of the best method to solve small instances of almost any combinatorial optimization problem. In addition, many sophisticated exact algorithms use plain enumeration as a subroutine, when during the search process the size of the problem becomes small enough.

Consider now the Maximum Clique Problem: Given an undirected graph $G=(V,E)$, the problem is to find the largest complete subgraph of $G$. More formally, you look for the largest subset $C$ of the vertex set $V$ such that for any pair of nodes ${i,j}$ in $C \times C$ there exists an arc ${i,j} \in E$.

The well-known branch-and-bound algorithm of Carraghan and Pardalos [2] is based on enumeration. The implementation of Applegate and Johnson, called dfmax.c, is a very efficient implementation of that algorithm. Next, I show a basic implementation of the same algorithm that uses CBack for backtracking.

The Carraghan and Pardalos algorithm uses three sets: the current clique $C$, the largest clique found so far $C^*$, and the set of candidate vertices $P$. The pseudo code of the algorithm is as follows (as described in [3]):

1
2
3
4
5
6
7
8
9
10
11
12
13

function findClique(C, P)
   if |C| > |C*| then C* <- C  // store the best clique
   if |C| + |P| > |C*| then
      for all v in P // the order does matter 
         P <- P \ {v}
         C' <- C u {v}
         P' <- P  \intersect N(v)  // neighbors of p
         findClique(C', P')

function main()
   C* <- {}  // empty set, C* global variable
   findClique({},V)
   return C*

As you can see, the backtracking is here described in terms of a recursive function. However, using CBack, we can implement the same algorithm without using recursion.

Maximum Clique with CBack

We use an array S of $n$ integers, one for each vertex of $V$. If S[v]=0, then vertex $i$ belongs to the candidate set $P$; if S[v]=1, then vertex $i$ is in $C$; if S[v]=2, then vertex $i$ cannot be neither in $P$ nor in $C$. The variable s stores the size of current clique.

Let me show you directly the C code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

for (v = 0; v < n; v++ ) {
   /// If the current clique cannot be extended to a clique
   /// larger than C*, where LB=|C*|, then backtrack
   if ( s + P <= LB )
      Backtrack();
   if ( S[v] < 2 ) {  /// Skip removed vertices  
      /// Choice: Either v is in C (S[v]=1) or is not (S[v]=2)
      S[v] = Choice(2);
      if ( S[v] == 2 ) { /// P <- P \ {v} 
         P--;  /// Decrease the size of the candidate set 
      } else { /// S[v]=1: C <- C u {v}
         s++;   /// Update current clique size 
         if ( s > LB ) {
            LB = s;  /// Store the new best clique
            for ( w = 0; w <= v; w++ )
               C[w] = S[w];
         }
         /// Restrict the candidate set 
         for ( w = V[v+1]; w > V[v] ; w-- )
            if ( S[E[w]] == 0 ) {
               S[E[w]] = 2;
               P--; /// Decrease the size of the candidate set 
            }
      }
   }
}
Backtrack();

Well, I like this code pretty much, despite being a “plain old” C program. The algorithm and code can be improved in several ways (ordering the vertices, improving the pruning, using upper bounds from heuristic vertex coloring, using induced degree as in [2]), but still, the main loop and the backtrack machinery is all there, in a few lines of code!

Maybe you wonder about the efficiency of this code, but at the moment I have not a precise answer. For sure, the ordering of the vertices is crucial, and can make a huge difference on solving the max-clique DIMACS instances. I have used CBack to implement my own version of the Ostengard’s max-clique algorithm [4], but my implementation is somehow slower. I suspect that the difference is due to data structure used to store the graph (Ostengard’s implementation relies on bitsets), but not in the way the backtracking is achieved. Although, to answer to such question could be a subject of another post.

In conclusion, if you need to implement an exact enumerative algorithm, CBack could be an option to consider.

References

1. Keld Helsgaun. CBack: A Simple Tool for Backtrack Programming in C. Software: Practice and Experience, vol. 25(8), pp. 905-934, 2006. [doi]

2. Carraghan and Pardalos. An exact algorithm for the maximum clique problem. Operations Research Letters, vol. 9(6), pp. 375-382, 1990, [pdf]

3. Torsten Fahle. Simple and Fast: Improving a Branch-and-Bound Algorithm. In Proc ESA 2002, LNCS 2461, pp. 485-498. [doi]

4. Patric R.J. Ostergard. A fast algorithm for the maximum clique problem. Discrete Applied Mathematics, vol. 120(1-3), pp. 197–207, 2002 [pdf]